Zavezniški letalci v cerkvenjaški zgodovini; urednik Marjan Žmavc, Slovenskogoriški forum, 2005

Usodni polet Donalda S. Morisona in članov posadke B-24

Med starejšimi Cerkvenjačani je še danes živa zgodba o strmoglavljenju ameriškega bombnika B-24 Liberator,19.03.1944 leta na Vanetini. To letalo je bilo še z mnogimi drugimi tistega dne na 12. misiji za 454. skupino bombnikov, in sicer z nalogo uničiti vojaške objekte v sosednji Avstriji. Zaradi močne protiletalske obrambe je bilo letalo zadeto, zato je pilot izdal povelje, da se misija prekliče. Po izjavah očividcev je to letalo zaostajalo za ostalimi in bilo nato napadeno še s starni dveh nemških lovcev. Bombnik je bil močno poškodovan; v letalu je odjeknila silovita eksplozija, ki je povzročila prelom levega krila pri drugem motorju. Letalo je kot velika goreča gmota strmoglavilo v vinograd pri Kurnikovih na Vanetini. Izmed desetih članov posadke se je s pravočasnim skokom iz letala uspelo rešiti le štirim letalcem. Ostalih šest letalcev je umrlo v razbitinah letala, med njimi je bil tudi kopilot Donald Schoenwether Morrison.

Več podrobnosti najdete v tej knjižici, kjer na 63 starneh opisujejo dogodke naslednji avtorji: Marjan Žmavc, mag. Ciril Paluc, mag. Marjan Toš, Edvard Pukšič, dr. Bernard Rajh in prof. Mirko Žmavc.

Del šolske etnografske zbirke:

Seminarske naloge iz matematike 8. razred
Seminarske naloge iz matematike 9. razred

Naloge za vajo (7. razred):

• Ulomki – vaje (J. Kumer) Ulomki-vaje_rešitve
• Vaje za preizkus znanja – trikotnik (J. Kumer)
• Rešitve vaj za preizkus znanja – trikotnik

Naloge za vajo (8. razred):

• Vaje: večkotniki, krog, Pitagorov izrek (J.Kumer)

Naloge za NPZ 9. razred:

• MAT2004
• MAT2005
• MAT2006
• MAT2008
• MAT2009
• MAT2010
• MAT2011
• MAT2012
• MAT2013
• MAT2014

Tekmovanje za Vegovo priznanje:

	Šolsko tekmovanje (bronasto priznanje)	1. – 9. razred	četrtek, 16. marec 2017, ob 1300 (I.triada ob 1100)
	Državno tekmovanje (srebrno priznanje) (zlato priznanje)	5., 6., 7., 8., 9. razred	sobota, 22. april 2017, ob 900

Spletne povezave:

DMFA – Društvo matematikov, fizikov in astronomov Slovenije: http://www.dmfa.si/
(na tej strani se nahaja elektronska revija Brihtnež z mnogimi vsebinami za dodatno učenje matematike in kot priprava na tekmovanja)

Fakulteta za matematiko in fiziko: http://www.fmf.uni-lj.si/
Pedagoška fakulteta Maribor: http://www.pfmb.uni-mb.si/
Presek: list za mlade matematike, fizike, astronome in računalnikarje: http://zaloznistvo.dmfa.si/presek/

Zanimivosti:
Eulerjev izrek: “Za število vozlišč, daljic in ploskev velja naslednja zveza: a + b – c = 1, kjer je

• a – število vozlišč
• b – število ploskev
• c – število daljic oz. povezav

Za različne primere preveri veljavnost.
Podobna zveza velja za telesa. Razišči!

Številski sistemi: število 2005

1. Število 2005 v različnih številskih sistemih:

Leto 2047 se bo v dvojiškem sistemu zapisalo s samimi enicami, in sicer:

2047 [10] = 11 111 111 111 [2],

že naslednja letnica 2048 pa bo naslednje oblike:

2048 [10] = 100 000 000 000 [2].

Iz zgornje tabele hitro najdemo še eno “lepo” številko, in sicer 2006 v trojiškem sistemu:

2006 [10] = 2202022 [3]

2. Število 2005 kot razcep na prafaktorje:

2005 = 5 . 401

3. Število 2005 kot razlika in vsota kvadratov:

2005 = 2032 – 1982 ( ??? – hm, kako se pa to najde )

2005 = 182 + 412

4. Zastavimo si nalogo in zapišimo število 2005 s samimi peticami (enicami,…). Tu navajam samo dve možnosti:

2005 = 55-555-555-5-5

2005 = 1111+11 . (1+1+1)1+1+1+1 +1+1+1

5. Z malo truda lahko pokažemo, da se 2005 ne da zapisati npr. kot:

2005 = 12 + 22 + 32 + 42 + …

2005 = 11 + 22 + 33 + 44 + …

Kmalu ali že sedaj lahko začnemo raziskovati število 2006, čeprav ne iščemo v tem numeroloških ali astroloških zakonitosti, pač pa enostavno odkrivamo matematične zakonitosti. Le te so že same zase dovolj lepe.
(S. Toplak)

Naloga množenja:

Videti je zahtevno, pa ni!
V nakazanem računu množenja zamenjaj kvadratke z desetiškimi števkami tako, da bo dobljeni račun pravilen.

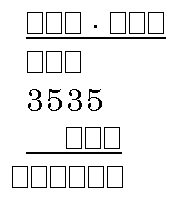Rešitev: – število 3535 je produkt prvega števila in sredinske števke drugega, zato sta možnosti tu dve, in sicer: 3535:5=707 in 3535:7=505, – prva in zadnja števka drugega ševila je 1, saj le tako dobimo produkt trimestno število, – na koncu še premislimo o obeh možnostih; da so v rezultatu popolnjena vsa mesta, je edina možnost: 707 . 151 = 106757.

Število trikotnikov:

Koliko trikotnikov je na sliki?

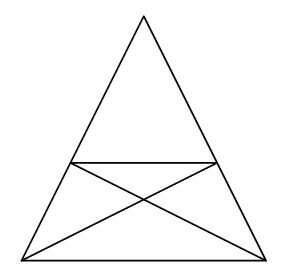Rešitev: 12 trikotnikov

“Tablice so svetovne”, učenci 8. razreda – skupina 2; 2014 (učilnica matematike)

• Preverjanje znanja – N. Grafenauer: Ljubezen

Tekmovanje za Cankarjevo priznanje

Spletne povezave:

Zavod RS za šolstvo – slovenščina:
http://www.zrss.si/default.asp?link=predmet&tip=6&pID=26

Slovar slovenskega knjižnega jezika

Slovar založbe DZS, d.d., ki je nastal v sodelovanju s SAZU, ZRC SAZU, Inštitutom za slovenski jezik Frana Ramovša in avtorji. Obsega več kot 100.000 gesel in podgesel, ki vsebujejo naslednje informacije: naglas, slovnične oznake, običajne zveze ter različne kvalifikatorje. Fraze in termini so opisani v posebnih gnezdih. SSKJ je do sedaj najobsežnejši slovar sodobnega slovenskega jezika. Več poglej na strani… (demo verzija): http://www.amebis.si/izdelki/sskj/